| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
Tags
- django
- Python
- 장고
- MEAN Stack
- M2M
- Visual Studio Code
- MX Component
- 오라클
- 윈도우10
- rs422
- rs485
- 자본주의
- sql developer
- c#
- 파이썬
- oracle
- vscode
- tensorflow
- scrapy
- matplot
- MSSQL
- Serial
- 티스토리 초대장
- 딥러닝
- 텐서플로우
- windows10
- MSSQL PYTHON
- 크롤링
- PYTHON MSSQL
- pymssql
Archives
- Today
- Total
안까먹을라고 쓰는 블로그
[Python과 텐서플로우를 활용한 딥러닝 기본 향상과정] 4일차 - Source 본문
반응형
-
Linear Graph
import numpy as np
import matplotlib.pyplot as plt
x = np.arange(0,5,0.1)
y1 = []
for value in x:
y1.append(value)
y2 = []
for value in x:
y2.append(2*value - 2)
y3 = []
for value in x:
y3.append(0.5*value + 1)
plt.plot(x, y1, label="y=x") ## 상단에 곡선 설명
plt.plot(x, y2, linestyle="--", label="y=2x-2") ## 점선으로 표시
plt.plot(x, y3, linestyle="--", label="y=0.5x+1") ## 점선으로 표시
plt.xlabel("x") ## x축에 표시되는 문자열
plt.ylabel("y") ## y축에 표시되는 문자열
plt.title("linear graph") ## 상단의 제목 표시
#plt.legend(loc='upper left') ## 범례 표시가 나타나는 위치 - 디폴트는 우측상단
#plt.legend(loc='lower left')
plt.show()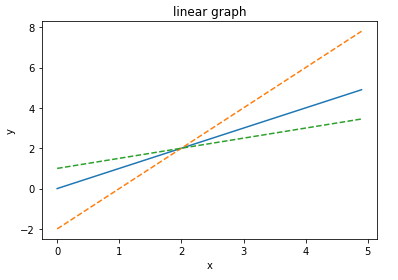
-
Cost Graph
### 선형분석 01
### h = wx 선형 함수에서 w에 대한 비용 곡선 -- 이게 선형 분석의 시작으로
# Lab 3 Minimizing Cost
import tensorflow as tf
import matplotlib.pyplot as plt
## %matplotlib inline ## 주피터 노트북에서 그림이 그려지지 않을때 넣어준다
#tf.set_random_seed(777)
X = [1, 2, 3] ## 예측치
Y = [1, 2, 3] ## 실제 결과값
W = tf.placeholder(tf.float32) ## 여기에 임의의 값을 넣어서 비용곡선을 만들 예정임
# 일단 쉬운 이해를 이해서 b(바이어스)는 생략하자
h = X * W
# 비용/손실 함수
cost = tf.reduce_mean(tf.square(h - Y)) ##tf.reduce_mean(tf.square(X*W - Y))
sess = tf.Session()
W_data = [] # 현재의 가중치를 닫을 그릇
cost_data = [] # 가중치에 대한 비용을 닫을 그릇
for i in range(-30, 50): ## -30~50 까지 1 단위로 증가
current_W = i * 0.1 ## 1단위를(int) ==> 0.1(float) 단위로
current_cost = sess.run(cost, feed_dict={W: current_W})
print(current_W, current_cost)
W_data.append(current_W)
cost_data.append(current_cost)
# Show the cost function
plt.plot(W_data, cost_data)
plt.xlabel("Weight")
plt.ylabel("Cost(W)")
plt.title("Weight - Cost(W)")
plt.show()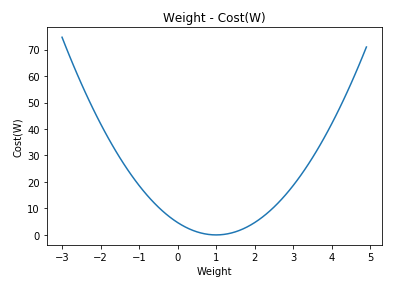
-
Sigmoid Graph
## sigmoid 함수 그래프
import numpy as np
import matplotlib.pyplot as plt
x = np.arange(-10, 10, 0.01)
y = []
y= 1 / (1 + np.exp(-x))
plt.plot(x, y, label="sigmiod(logistic)") ## 상단에 곡선 설명
plt.xlabel("x") ## x축에 표시되는 문자열
plt.ylabel("y") ## y축에 표시되는 문자열
plt.title("sigmiod(logistic) graph") ## 상단의 제목 표시
plt.legend(loc='upper left') ## 범례 표시가 나타나는 위치 - 디폴트는 우측상단
plt.show()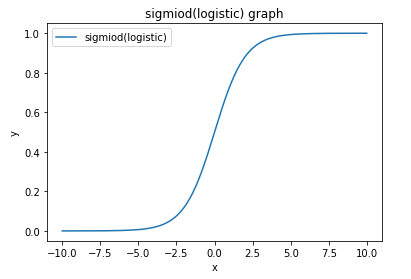
-
Logistic Normal Cost Graph
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
X = [1, 2, 3, 4, 5, 6] ## 예측치
#X = [[1, 2],[2, 3],[3, 1],[4, 3],[5, 3],[6, 2]]
Y = [0, 0, 0, 1, 1, 1] ## 실제 결과값
W = tf.placeholder(tf.float32)
z = W * X
h = []
h = 1 / (1 + tf.exp(-z))
cost = tf.reduce_mean(tf.square(h - Y))
sess = tf.Session()
W_data = [] # 현재의 가중치를 닫을 그릇
cost_data = [] # 가중치에 대한 비용을 닫을 그릇
for i in range(-50, 50): ## -30~50 까지 1 단위로 증가
current_W = i * 0.1 ## 1단위를(int) ==> 0.1(float) 단위로
current_cost = sess.run(cost, feed_dict={W: current_W})
print(current_W, current_cost)
W_data.append(current_W)
cost_data.append(current_cost)
# Show the cost function
plt.plot(W_data, cost_data, label="cost = tf.reduce_mean(tf.square(h - Y))")
plt.xlabel("Weight")
plt.ylabel("Cost(W)")
plt.title("h = 1 / (1 + exp(-WX)) : Weight - Cost(W)")
plt.legend(loc='center left')
plt.show()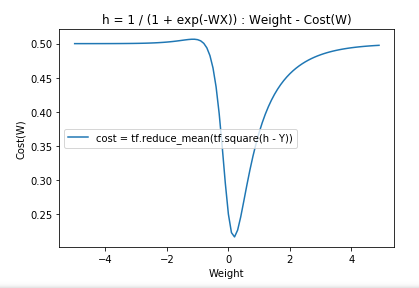
-
Log Graph
## -log(x), -log(1-x) 함수 그래프
import numpy as np
import matplotlib.pyplot as plt
x = np.arange(0.01, 1, 0.01)
y1 = -np.log(x)
y2 = -np.log(1-x)
plt.plot(x, y1, label="y = -log(x)") ## 상단에 곡선 설명
plt.plot(x, y2, label="y = -log(1-x)") ## 상단에 곡선 설명
plt.xlabel("x") ## x축에 표시되는 문자열
plt.ylabel("y") ## y축에 표시되는 문자열
plt.title("log graph") ## 상단의 제목 표시
plt.legend(loc='upper center') ## 범례 표시가 나타나는 위치 - 디폴트는 우측상단
plt.show()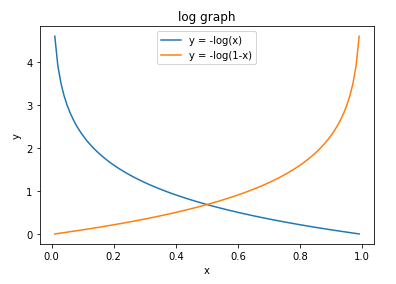
-
Logistic Log Cost Grpah
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
#x = np.arange(-2.0, 2.01, 0.01)
X = [1., 2., 3., 4., 5., 6.] ## 예측치
Y = [0, 0, 0, 1, 1, 1] ## 실제 결과값
W = tf.placeholder(tf.float32)
z = W * X
h = []
h = 1 / (1 + tf.exp(-z))
cost1 = tf.reduce_mean(-tf.log(h))
cost2 = tf.reduce_mean(-tf.log(1 - h))
sess = tf.Session()
W_data = [] # 현재의 가중치를 닫을 그릇
cost1_data = [] # 가중치에 대한 비용을 닫을 그릇
cost2_data = []
for i in range(-30, 31): ## -30~50 까지 1 단위로 증가
current_W = i * 0.1 ## 1단위를(int) ==> 0.1(float) 단위로
current_cost1 = sess.run(cost1, feed_dict={W: current_W})
current_cost2 = sess.run(cost2, feed_dict={W: current_W})
print(current_W, current_cost1, current_cost2)
W_data.append(current_W)
cost1_data.append(current_cost1)
cost2_data.append(current_cost2)
# Show the cost function
plt.plot(W_data, cost1_data, label="cost = -log(h), Y=1")
plt.plot(W_data, cost2_data, label="cost = -log(1-h), Y=0")
plt.xlabel("Weight")
plt.ylabel("Cost(W)")
plt.legend(loc='upper center')
plt.title("cost(w) = Y * tf.log(h) + (1 - Y) * tf.log(1 - h) ")
plt.show()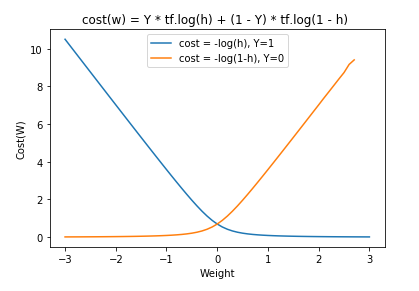
반응형
'Language > Python' 카테고리의 다른 글
| [Python과 텐서플로우를 활용한 딥러닝 기본 향상과정] 5일차 (0) | 2019.11.09 |
|---|---|
| TensorFlow 함수정리 (0) | 2019.11.02 |
| [Python과 텐서플로우를 활용한 딥러닝 기본 향상과정] 4일차 (0) | 2019.11.02 |
| [Python과 텐서플로우를 활용한 딥러닝 기본 향상과정] 3일차 (0) | 2019.10.26 |
| [Python] 모두의 데이터분석 with 파이썬 - 코드2 (matplot) (0) | 2019.10.21 |
Comments